Maubeuge les 20, 21 et 22 septembre 2000
par Richard Denner
|
« Le savoir ne peut pas se passer de la beauté. Je
cherche une science belle. » « À partir d'un certain âge de son histoire, la science doit répondre de son visage, de la beauté qu'elle présente et produit. » Michel Serres*, Les cinq sens, p 133. |
En septembre 2000, la ville de Maubeuge a accueilli un colloque sur le thème :
« Comment les Arts peuvent-ils venir en aide à l'enseignement des Mathématiques ? »
Laissons à Claude-Paul Bruter** (professeur à l’Université Paris 12 et initiateur du projet ARPAM***) le soin de présenter les objectifs du Colloque(1):
« L’objectif central du Colloque est de nature pédagogique. De manière subtile, il voudrait concerner la formation de l’esprit. De façon plus apparente, il tourne autour de la transmission et de l’acquisition des connaissances à travers des représentations visuelles, qu’elles soient statiques comme la peinture, la sculpture ou l’architecture ou bien plus dynamiques, comme les animations audio-visuelles, la qualité de ces représentations étant soutenue par les ressources de l’art musical et de l’art littéraire. »
Permettre à chacun de se forger sa propre idée en faisant la synthèse des faits qui m’ont le plus marqués en tant que professeur de collège tel est le but de cet article qui contient un nombre important de liens Internet.
La recherche d’approches pédagogiques nouvelles qui faciliteraient l’apprentissage et l’assimilation en constitue la toile de fond.
1. Regard sur le colloque au travers de l’enseignement en classes de collège.
De tout temps, la réalisation de belles figures a fasciné les géomètres. Les dessins que l’on découvre dans les cavernes préhistoriques(2) continuent d’exercer un attrait mystérieux sur l’homme contemporain qui dispose des ordinateurs(3) les plus performants pour visualiser les objets de ses études. Pourtant, au moment où l’on détient les moyens technologiques les plus avancés, les conditions d’enseignement deviennent plus difficiles.
Au niveau du collège, les professeurs sont amenés à accueillir des élèves dont les profils sont de plus en plus variés. Il s’agit non seulement de transmettre des connaissances mais surtout, de développer des compétences et des attitudes qui permettent l’apprentissage.
La géométrie offre une approche intéressante des mathématiques [1] : de part les constructions qu’elle permet de faire, elle suscite l’attrait et provoque le questionnement. Bien plus que cela par ailleurs, avec l'arithmétique, elle en constitue l'un des deux chapitres fondamentaux.
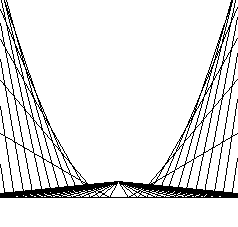
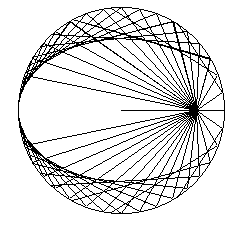
Quand les jeunes élèves commencent à faire leurs premiers tracés avec la règle et l’équerre, ils peuvent être sensibilisés à l'esthétiques des courbes mathématiques. La construction de paraboles, d’ellipses voire d’hyperboles comme enveloppes de leurs tangentes est à la portée d’un collégien. En traçant des traits droits, ils ont la surprise de voir apparaître des courbes connues depuis l’antiquité grecque.


Parabole et ellipse
En agissant avec leurs mains, les élèves peuvent se confronter avec les difficultés de la figure qu’ils sont en train de dessiner ; les questions surgissent naturellement, la matière résiste. Quand ils aboutissent, ils éprouvent un réel plaisir et peuvent dévoiler leur travail aux regards des autres. Cette démarche ne ressemble-t-elle pas à celle de l’artiste ? Pour vous en convaincre, découvrez les magnifiques sculptures symboliques John Robinson(4) et toute la beauté qu’elles dégagent.
Un autre domaine qui fascine les enfants est celui de la construction de polyèdres ; quand pour la première fois ils fabriquent un solide en partant de son patron, c’est toujours avec étonnement qu’ils le voient prendre forme entre leurs doigts. Les adultes également sont séduits par la vue des polyèdres. George W.Hart(5), sculpteur américain en a fait sa passion, son site Internet est d’une très grande richesse. On y découvre de nouveaux polyèdres ainsi que de multiples façons, parfois inattendues, de les assembler.
Il y a quelques années, les bracelets brésiliens étaient à la mode. En réalité, l’usage des nœuds et des cordages remonte à la préhistoire. Comme l’a montré Ronnie Brown(6), il est possible de les utiliser dans l’enseignement en faisant l’analogie entre la théorie des nœuds et l’algèbre.
Les bulles de savons(7) cachent également plus de mathématiques qu’on pourrait le penser. Isolées, elles sont des sphères parfaites. Quand elles s’assemblent par deux, trois ou plusieurs elles révèlent le monde des surfaces minimales. Dans sa vidéo « Touching Soap Films (8)», Konrad Polthier(9) nous invite à les découvrir. En 1760, Lagrange posa le premier le problème : étant donné un bord de forme quelconque, existe-il une surface d’aire minimale s’appuyant sur ce bord ? Une boucle quelconque en fil de fer plongée dans de l’eau savonneuse, fera immédiatement apparaître la solution. Une description de ce phénomène est donnée par Nathaniel Friedman(10) qui montre, à la manière de Spivak dans le volume IV de son traité de géométrie différentielle, comment on peut ainsi générer un ruban de Möbius.
L’architecture, avec la construction de toitures qui soient les plus légères possibles, en est un domaine d’application privilégié. Un exemple typique est la construction du stade olympique de Munich.
La visualisation des surfaces et des solides est rendue très conviviale à l’aide du logiciel JavaView(11) mis au point à l’Université Technique de Berlin, il peut être téléchargé par Internet. Il est également possible de consulter et de soumettre des modèles sur le site Electronic Geometry Models(12).
Le thème des pavages n’est pas nouveau dans les classes de collège. En étalant le travail sur une durée suffisamment longue, il est possible que les élèves conçoivent leur propre chef d’œuvre en utilisant par exemple la technique de l’enveloppe [2]. Mike Field(13) utilise des ordinateurs pour créer des pavages, non pas de manière statique, mais, c'est nouveau par rapport aux méthodes anciennes, en utilisant des systèmes dynamiques présentant des symétries.
Il révèle des motifs fascinants qui provoquent l’admiration, encouragent l’observateur à développer ses propres capacités et l'incite à rechercher des idées nouvelles.
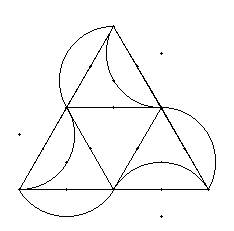 Une
autre source d’inspiration est l’art arabe(14). En pénétrant avec Antonio F. Costa(15) dans les murs de l’Alhambra de Grenade(16)on y découvre mille
merveilles, notamment les pavages(17) du plan qui sont autant de
chefs d’œuvre de finesse et d'ingéniosité.
Une
autre source d’inspiration est l’art arabe(14). En pénétrant avec Antonio F. Costa(15) dans les murs de l’Alhambra de Grenade(16)on y découvre mille
merveilles, notamment les pavages(17) du plan qui sont autant de
chefs d’œuvre de finesse et d'ingéniosité.
J’ai retenu en particulier un exemple qui me semble réalisable par des élèves de cinquième. Les premières réalisations furent encourageantes. On reconnaîtra aisément la construction du motif de base ci-contre à partir des quatre triangles équilatéraux.
La piste suivie par Maria Dedo'(18) est très intéressante car elle met facilement en contact avec la théorie des groupes. Elle utilise des miroirs(19) pour visualiser des pavages et des polyèdres. Le motif de base, par réflexion dans trois miroirs, remplit tout le plan ou permet de visualiser un polyèdre dans l’espace comme on a pu le voir lors de la récente exposition « Math.u-vu ? »(20) organisée par l’Irem de Strasbourg.
Dans sa vidéo « The Optiverse » John Sullivan(21) a présenté sa dernière version du retournement de la sphère(22).
De magnifiques images qui suscitent l’imagination ! La sphère se déforme sans se déchirer, sa surface se traverse elle-même, sa face interne et sa face externe apparaissent en même temps à celui qui suit la déformation. Le tout passe par une étape centrale puis un chemin semblable conduit à la sphère retournée.
Quelle belle invitation à dépasser ses propres limites !
Les tableaux faits avec des fils tendus entre des clous sont bien connus ; leur attrait provient des courbes dont l’arrangement permet de produire les motifs les plus variés.
Les mathématiciens utilisent des méthodes analogues pour engendrer des surfaces. Les surfaces réglées en sont un exemple typique, elles sont générées par des droites. On peut les matérialiser en assemblant des segments métalliques comme le fait Philippe Charbonneau(23) pour construire des surfaces réglées du troisième degré dont l’aspect esthétique retient le regard et fascine. Il en est de même des tracés pendulaires obtenus par l’artiste et qui se situent dans le sillage des entrelacs [3] dont l’origine remonte à la préhistoire.
Une autre méthode permettant de visualiser les surfaces réglées consiste à tendre du fil à coudre entre deux plaques parallèles comme l’a expliqué François Apéry(24) au cours de son intervention. Il utilise également des ellipses en fil de fer pour visualiser des surfaces et en particulier son modèle central du retournement de la sphère. Il a soigneusement expliqué comment on fabriquait ce genre de modèles qui demandent précision et minutie.
Au cours d’un des ateliers, j’ai présenté mon diaporama sur le retournement du cuboctaèdre. Il illustre les principales étapes de la déformation et permet de comprendre les transformations qui se succèdent à l’intérieur des modèles construits en carton bicolore et en plastique transparent.
Prises au téléobjectif et en lumière artificielle, ces diapositives complètent mon article paru dans L'Ouvert n°94(25) et n°95(26). L’ensemble des modèles était également exposé ; John Sullivan en a pris quelques photos(27) visibles sur une des ses pages Web.
Une des séquences de « The Optiverse » illustre la version du retournement du cuboctaèdre(28) réalisée par François Apéry en 1992. Elle se résume en une simple interpolation linéaire entre le modèle central et le modèle de départ. (F. Apéry, G. Francis, C. Hartman and G. Chappell, University of Illinois at Urbana-Champaign.)
Je terminerai ici cette première partie en citant les travaux du graveur sur cuivre Patrice Jeener(29) avec qui je me suis longtemps entretenu. Il a également été passionné par la bouteille de Klein et la surface de Boy dont il a fait de magnifiques lithographies. Sa triple bouteille unilatère est particulièrement remarquable. Certaines de ses images ont donné lieu à des animations sur ordinateur réalisées par Jean-François Colonna(30).
2. L’enseignement des mathématiques a-t-il besoin de l’apport de l’art ?
Les brochures de l’APMEP(31) font depuis longtemps une large part à l’activité de l’élève. On pourrait penser au premier abord que ce côté « artistique » soit inutile voire superflu. Comme le souligne Xah Lee(32), mathématicien américain, l’admiration d’une belle image fractale n’apprend rien sur les mathématiques sous-jacentes ! En parcourant le site qu’il a indiqué, on découvrira de multiples aspects de l’activité mathématique. La recherche de problèmes en fait leur essence même.
Dans une brochure éditée par l’Irem de Reims en 1986 [4], Michèle et André Arsène recherchent des applications de l’œuvre de Jean Piaget à l’enseignement au collège. Je n’en citerai que quelques extraits dus à Piaget lui-même :
« L’enfant retient ce qu’il a compris et non pas ce qu’il a vu, et ce n’est pas si naturel qu’on pourrait le penser. » p 92
« L’action propre donne de meilleurs résultats que la perception et l’apprentissage dans l’ordre action -----> perception réussit mieux que dans l’ordre perception -----> action. » p 92
« … la représentation ne remplace vraiment l’action qu’après avoir été suffisamment informée par l’action elle-même, et l’on ne saurait ainsi, sans une coupure artificielle, la détacher de son contexte actif, pas plus que l’on ne peut dissocier une perception de son contexte sensori-moteur. » p.61
« Il n’y a de progrès pour nul écolier au monde, ni en ce qu’il entend, ni en ce qu’il voit, mais seulement en ce qu’il fait ». Alain. p 96
« En un mot, dès qu’il s’agit de la parole ou d’enseignement verbal, on part du postulat implicite que cette transmission éducative fournit à l’enfant les instruments comme tels de l’assimilation, en même temps que les connaissances à assimiler, en oubliant que de tels instruments ne peuvent s’acquérir que par une activité interne et que toute assimilation est une restructuration ou une réinvention. » p 91
« C’est précisément parce que ces connaissances sont tirées des actions et non pas des objets comme tels qu’elles peuvent dans la suite être traduites en opérations symboliques et en langage. » p 73
Parlant de l’apprentissage, les auteurs notent que : « toute la difficulté est de trouver des activités qui permettront aux élèves de mettre en place leurs propres structures logiques, petit à petit, dès la classe de 6ème, en les faisant agir sur des objets géométriques par exemple, mais surtout sans vouloir formaliser trop vite ». p 36
Il me semble que ces quelques phrases peuvent servir de repères dans la recherche d’améliorations des pratiques pédagogiques. Quel peut alors être le rôle des arts ?
C’est la multiplicité des profils des élèves qui peut amener à diversifier les modes d’approches. De plus en plus on rencontre des jeunes qui traversent des moments difficiles, les situations qu’ils vivent parfois ne favorisent pas leur parcours scolaire et souvent les empêchent de fixer leur attention. Comment prendre en compte cette instabilité ? Une simple activité intellectuelle peut-elle la contrebalancer ? Les mathématiques peuvent-elles leur laisser une impression qui ne soit pas forcément synonyme d’échec ?
Une des critiques formulées par David Cohen dans [5] à l’encontre de Piaget est de négliger l’aspect affectif et l’influence de la société sur l’évolution de l’enfant. Or actuellement, les comportements des jeunes semblent dire qu’ils ne sont pas négligeables.
Les images que l’on a pu voir au colloque, issues de l’imagination et du travail des mathématiciens mais également fabriquées des mains des artistes, exercent un pouvoir d’attraction sur l’observateur. C’est comme si soudain les mathématiques elles-mêmes devenaient tangibles, on peut d’un coup d’œil appréhender ce qui était dans l’imaginaire. L’objet mathématique devient objet réel, rempli de toute l’information que l’artiste y a déposée. Enrichi par tout le temps accumulé, il peut s’inscrire dans la durée.
Avec Manuel Arala Chaves(33), professeur à Porto et membre du comité organisateur du colloque, découvrons le site « atractor »(34) de l’Université de Lisbonne. On y trouvera en particulier une très belle collection de polyèdres ainsi que des animations sur le ruban de Möbius. À noter également une introduction aux représentations par des modèles réels des surfaces mathématiques complétée par une étude de leur orientation.
Rendre les mathématiques interactives est un des objectifs de l’association qui gère le site. La réalisation d’une exposition itinérante est à l’étude dans le cadre d’un projet européen. Des liens vers d’autres sites participant au projet ainsi que vers des musées scientifiques à travers le monde s’y trouvent.
Avec les possibilités des multimédias, la tentation de passer d’un sujet à un autre sans approfondissement représente un écueil certain ; cependant, ils ouvrent de multiples horizons et permettent d’aller à la rencontre des artistes et des chercheurs en faisant connaître leurs travaux.
C’est dans cette ouverture nouvelle que l’on peut mieux situer le débat de l’influence de l’art sur l’enseignement des mathématiques.
La réalisation d’une œuvre d’art mobilise tous les talents de l’artiste adulte, n’en pourrait-il pas être de même pour nos élèves ? Pour aboutir, de nombreux problèmes doivent être résolus et ce n’est qu’avec le temps et de très nombreuses approches successives que l’on arrive au bout du chemin. En leur proposant une « œuvre » à leur portée, ils pourraient y exprimer de nombreuses potentialités et éprouver la joie que procure sa réalisation tout en faisant fonctionner les mathématiques sous-jacentes.
En somme, les arts ne pourraient-ils pas devenir facteur déclencheur de l’apprentissage en suscitant l’activité réelle de l’élève au sens où l’a décrite Piaget ?

Assemblage de six motifs élémentaires pour un modèle visible(35) à l’Alhambra.
3. Quelques approches en classes de collège
Depuis de nombreuses années, depuis ma rencontre avec Bernard Morin(36), je fais réaliser par mes élèves, parallèlement aux cours habituels, des dessins géométriques qui illustrent telle ou telle propriété. Elles sont en grandes parties tirées des tomes 1 à 4 de l’ouvrage « La géométrie … pour le plaisir » de Lysiane et Jocelyne Denière [6]. L’aspect esthétique de la géométrie peut se révéler être source de motivation : des élèves en difficulté s’impliquent dans leurs productions.
Repris par mes collègues professeurs de mathématiques de la Providence-Nord et grâce aux conseils des professeurs d’arts plastiques, ces travaux donnent chaque année de belles réalisations.
Certains élèves montrent très rapidement de réelles capacités. Pour la plupart, les progrès viennent avec le temps. L'intérêt de ces élèves grandit d'années en années. C'est avec un réel plaisir qu'ils demandent à faire de nouveaux dessins.
Le pouvoir d’attraction des figures est ressenti par les enfants, naturellement ils dessinent des rosaces. Une attitude de recherche peut être provoquée par la découverte d’une construction qui ne leur est pas familière.
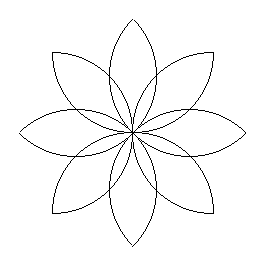
C’est le cas de la rosace ci-contre, extraite du bulletin APMEP n° 371[7], elle a eu un certain succès dans une classe de 6ème malgré la grande hétérogénéité des élèves alors que d’autres essais préliminaires furent moins bien réussis.Bien que turbulents par ailleurs, certains élèves ont montré une rapidité et une qualité d’exécution remarquable. Il a ainsi été possible de mettre en place un vocabulaire de géométrie élémentaire ainsi que, après plusieurs semaines, la rédaction du programme de la construction.
Les tracés de courbes point par point et par tangentes permettent également de belles réalisations.
Au cours de l’année scolaire précédente j’avais retenu, en classe de 6ème, le thème des courbes mathématiques. Inspiré des travaux de l’Irem de Strasbourg [8] et de la brochure de présentation des nouveaux programmes [9], ce travail s’est révélé fructueux.
Il montre qu’avec le simple matériel de géométrie habituel, il est possible d’amener de très jeunes élèves à exécuter des tracés très précis. Ils se familiarisent ainsi avec des courbes dont l’étude se prolonge jusqu’à l’université.
Les exemples sont classiques comme la cardioïde, l’astroïde et la rosace à quatre branches, l’ovale, l’ellipse, la parabole, mais aussi la cissoïde, la strophoïde droite, la cubique d’Agnesi [10] et la cubique anguinea voire la trisectrice de Mac-Laurin ou la spirale de Théodore de Cyrène [11].
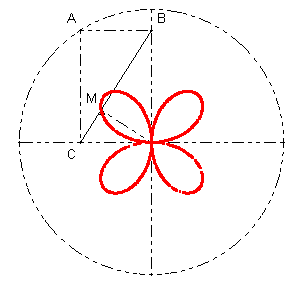
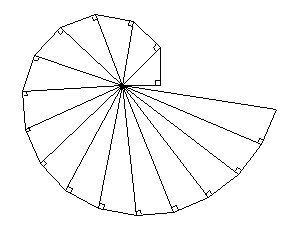
Spirale de Théodore de Cyrène et rosace à quatre branches
Il me revient à l’esprit le cas d’un élève qui savait à peine manipuler l’équerre en début d’année et qui de semaines en semaines a fait de beaux progrès ; mais d’autres également qui ont très rapidement fait preuve d’excellentes qualités graphiques.
La répétition d’un même geste est ici un élément essentiel, il favorise l’acquisition des représentations internes des concepts.
On trouvera sur le site de Jean-Paul Quelen(37), professeur au lycée Jean Monnet de Strasbourg, des animations de quelques-unes de ces courbes ainsi que bien d’autres thèmes mathématiques.

Construction : quand le point M décrit la droite (D) le point P décrit la cubique d’Agnesi.
Les pavages [12] offrent en 5ème des approches intéressantes. Après avoir expliqué le motif de base indiqué précédemment, il n’est pas très difficile de passer au plan entier à l’aide du pavage triangulaire pour obtenir le dessin ci-dessous qui peut être colorié selon les goûts de chacun :

Pavage(38) réalisé par les élèves de 5èmes.
On prépare ainsi l'apprentissage des transformations géométriques ; l’utilisation du papier calque est très utile dans cette démarche car elle permet de mettre en évidence, en agissant, qu’une symétrie centrale correspond à une rotation d’un demi-tour. Certains élèves observent que si l’on enchaîne deux symétries centrales le motif est simplement décalé.
Il a été possible d'aller plus loin à partir d'un retour sur l'étude de la symétrie axiale vue en 6e. En prenant comme point de départ le pavage « des petits chinois d’Escher(39)» ([2] ou [13]), il a été envisageable d’introduire la technique de l’enveloppe. Après un temps de maturation certain et une utilisation intensive du papier calque, les élèves ont pu créer leur propre pavage.
La démarche est semblable à celle suivie par des élèves de cinquième au cours d’un parcours diversifié(40) au collège Marcel Pagnol de Vernouillet dans l’académie d’Orléans-Tours.
Certaines réalisations furent particulièrement remarquables, et témoignent de réels talents. Les conseils des professeurs d’arts plastiques constituent à ce niveau d’avancement une aide précieuse pour les élèves qui peuvent ainsi mettre en œuvre toutes les ressources de leur imagination. De jour en jour, mais plutôt de semaine en semaine on voit poindre des améliorations dans les tracés et la finition mais également dans la création des modèles dont certains sont devenus très élaborés.
Par la suite, en 4ème et 3ème l’étude des translations et l’introduction des vecteurs sera grandement facilitée.
Les règles de la perspective cavalière peuvent être expliquées dès les premières années du collège et initient les élèves aux représentations spatiales. Le fichier « Pratiquer la géométrie. » [14] de l’Irem de Lorraine est apprécié depuis de nombreuses années par les élèves et les professeurs de notre établissement. Il favorise le travail indépendant introduit agréablement la géométrie dans l’espace.
Un travail qui a été motivant en début de 5ème a consisté à fabriquer un prisme droit à base hexagonale en papier blanc puis de faire réaliser, en perspective cavalière, le dessin d’un assemblage de plusieurs de ces prismes droits ayant des hauteurs différentes.
Au cours du colloque Dick Termes(41) [15] a expliqué comment représenter sur une sphère la globalité de ce que voit un observateur placé en un lieu donné en regardant dans toutes les directions ; il utilise ainsi une perspective avec six points de fuite ! Un exemple typique est la représentation de l’intérieur de la Sainte-Chapelle à Paris ou celle de la basilique Saint-Pierre à Rome.
Au collège des dessins avec un ou deux points de fuite sont possibles et permettent un parallèle fructueux avec les cours d’arts plastiques. Pour aller plus loin, Nicole Vogel(42), professeur au LEGT de Haguenau, propose sur son site quelques belles balades mathématiques, des excursions animées dans l’espace et une initiation au dessin en perspective.
Une initiation aux représentations en perspective cavalière du cube s'est avérée fructueuse en prenant comme point de départ l’ouvrage « Dessiner l’espace » de Michel Rousselet [16]. Il a été ainsi possible d’introduire les règles de dessin à respecter et de préparer une utilisation future des logiciels de dessin. En prolongement, on pourra envisager de représenter quelques troncatures du cube ainsi que des polyèdres(43) comme le tétraèdre régulier, l’octaèdre régulier ou le cuboctaèdre.
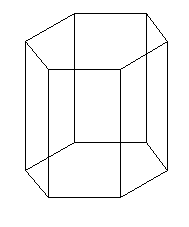

Prisme droit à base hexagonale et octaèdre régulier inscrit dans un cube
En fin d'année, la participation à l'Exposcience Alsace 2001 a suscité d'autres développements. L'assemblage de polyèdres à l'aide de tiges et de noeuds a permis de fabriquer les cinq polyèdres réguliers de Platon, quelques polyèdres semi-réguliers et les cinq polyèdres du mathématicien russe Fedorov qui permettent de paver l'espace(44). Une allusion à la cristallographie(45) à ainsi pu être faite. Ces polyèdres sont le cube (pyrite),le prisme droit à base hexagonale (orgues basaltiques), l'octaèdre tronqué encore appelé "polyèdre de Lord Kelvin", le dodécaèdre allongé et le dodécaèdre rhombique (grenat).
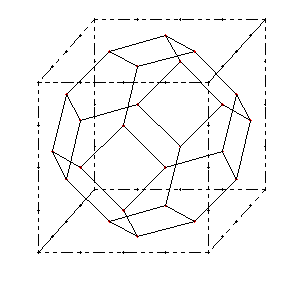
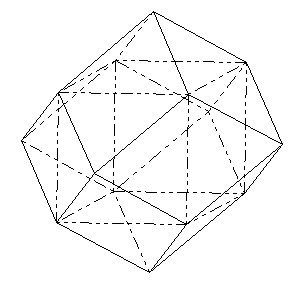
Polyèdre de Lord Kelvin et dodécaèdre rhombique
Ainsi, il a été possible de poser en introduction la question suivante,qui renvoyait également à d'autres stands.
"Comment la Nature remplit-elle l'espace, avec quels objets, pourquoi ?"
Ces quelques exemples, tirés de la pratique quotidienne sont autant de tentatives pour présenter la géométrie de façon attrayante à travers des activités qui visent la construction progressive des connaissances. Les aboutissements sont de « petits chefs-d’œuvre » exposables comme ceux de l’artiste adulte.
Remerciements :
Ce travail n'aurait pas pu être mené à son achèvement sans la participation active des élèves, d'anciens élèves, de collègues qui se sont spontanément associés au projet initial, et de parents d'élèves qui ont accepté d'assurer quelques contraintes matérielles. Je les en remercie vivement.
4. Conclusion
Le colloque ouvre de nombreuses voies, chacun pourra les parcourir à sa guise, y trouver maintes sources de curiosité, d’enrichissement et d’approfondissement. On peut sans doute y découvrir des voies d'exploration utiles à la mise en place des itinéraires de découverte dans les collèges, et des sujets d'étude pour les travaux personnalisés encadrés (TPE)(46).
Une œuvre d’art, la résolution d’un problème, sont de longs cheminements, des aboutissements. Artistes et chercheurs sont des personnes entièrement engagées dans le courant qui les porte vers l’accomplissement de leur ouvrage. Ils font confiance en leur expérience propre et en l’évaluation interne du travail qu’ils sont en train de réaliser.
Faire en sorte que l’élève puisse mener à son terme une œuvre personnelle, si petite soit-elle, au contact d’un professeur me semble être un complément intéressant aux nouvelles technologies. Cette démarche qui permet le développement de la créativité personnelle tout en exigeant persévérance et ténacité, s'apparente à celle de l'artiste et du chercheur.
Comme l’a fait remarquer Claude-Paul Bruter, l’œuvre achevée, exposée, crée une stabilité, un équilibre. L’œil de l’observateur revient se poser souvent sur elle pour en saisir les plus infimes détails. De même, la main du sculpteur, celle du géomètre, du mathématicien aveugle, perçoit les moindres variations de la courbure de la surface qu’elle effleure.
Des pyramides d’Egypte à la pyramide du Louvre(47), de l’art rupestre aux plus belles images fractales, Arts et Mathématiques marquent leur temps et sont les témoins de l’ingéniosité des hommes qui les ont fait naître. Puissent-ils être des exemples pour nos élèves en les incitant à développer le goût du beau et de la recherche(48).
Bibliographie :
Mathematics and Art, Actes du Colloque de Maubeuge, C.P.Bruter ed.,Springer -Verlag, Berlin, 2002 (volume de la série Mathematics and Visualisation)
Cet article à fait l'objet d'une publication voisine dans le numéro 103 de la revue L'Ouvert de l'Irem de Strasbourg(49) et dans le numéro 436 du bulletin de l'APMEP.
[1] Bulletins n°430 et n° 431 de l’APMEP.
[2] Activités
mathématiques en classe de quatrième-troisième, tome II.
Brochure Apmep n°38. p 79 à 115.
[3] Théorie des nœuds
et enluminures celtes. Christian Mercat.
L’Ouvert n° 84. p 1 à 22.
[4] Michèle et André ARSENE : Jean Piaget et les mathématiques au collège. IREM de Reims, Moulin de la Housse, 51100 REIMS.
[5] Faut-il brûler Piaget ? David Cohen. RETZ. Paris.
[6]La géométrie … pour le plaisir. Tome 1 à 4. Editions KIM, 26, rue Jules-Degroote, 59 240 Dunkerque.
[7] Bulletin APMEP n°371. p659 à 670. Géométrie, une approche par le dessin géométrique cm2-6ème. Yves Ducel, Marie-Lise Peltier.
[8] Activités géométriques de la sixième à la terminale. IREM de Strasbourg
[9] Mathématiques en classe de Sixième. La mise en œuvre des programmes de 96. Fascicule 2. Académie de Strasbourg.
[10] L’Ouvert n°96, p 47 à 50
[11] Les spirales, André Stoll, L’Ouvert n°96 p 1 à 13 et n°97 p 1 à 15.
[12] Le secret des pavages RAOUL RABA, Editions du PLOT.
[13] Maths en scène. Brochure APMEP n° 121.
[14] Pratiquer la Géométrie. Classe de 6éme et classe de 5ème. Fichier de l’Irem de Lorraine. Belin.
[15] New perspective système, seing the total picture, one through six point perspective by Dick A.Termes. (605) 642-4805, Route 2 Box 435 B, Spearfish, SD 57783, USA.
[16] Dessiner L’espace ou Comment employer Cabri-Géomètre dans l’espace, Michel Rousselet. Editions Archimède.
ARPAM : Association pour la Réalisation et la Gestion du Parc de Promenade et d'Activités Mathématiques.
Les figures de cet article sont faites avec le logiciel gratuit Déclic(50).
Lien supplémentaire
proposé par Emmanuel Ostenne concepteur du logiciel Déclic :
sur http://lilimath.free.fr il y a un lien vers GeoLap en Java
:représentation de patrons, de solides et pliage/dépliage de
patrons en langage Logo.
Et pour terminer, voici deux derniers liens suggérés par François Pluvinage vers des sites où l'on découvrira des dissections géométriques de polygones réalisés dans le cadre du projet CabriJava.
http://www.cabri.net/abracadabri/Coniques/Panoplie/Dissect/dissectG.htm
http://www.cs.purdue.edu/homes/gnf/book/webdiss.html
Adresses Internet :
* http://www.archipress.org/press/atlas.htm
** http://arpam.free.fr/bruter.html
*** http://arpam.free.fr/
(1) http://arpam.free.fr/colloque.html
(2) http://www.bradshawfoundation.com
(3) http://www.zib.de/vgp//
(4) http://www.popmath.org.uk/sculpture/sculpture.html
(5) http://www.georgehart.com/index.html
(6) http://www.popmath.org.uk/centre/index.html
(7) http://www.unice.fr/LEML/coursJDV/morpho/morpho3-2.htm
(8) http://www-sfb288.math.tu-berlin.de/~konrad/booklet/intro.html
(9) http://www-sfb288.math.tu-berlin.de/~konrad/video.html
(10) http://arpam.free.fr/friedman.html
(13) http://nothung.math.uh.edu/~mike/
(14) http://tecfa.unige.ch/tecfa/teaching/UVLibre/9900/bin08/welcome.htm
(15) http://www.maa.org/reviews/twovideos.html
(16) http://www.vivagranada.com/fr/index.htm
(17) http://weasel.cnrs.humboldt.edu/~spain/gran/index.htm
(18) http://arpam.free.fr/dedo.html
(19) http://specchi.mat.unimi.it/
(20)http://irem.u-strasbg.fr/irem/site00-01/annee2000/depliant/Mathuvu.html
(21) http://new.math.uiuc.edu/optiverse
(22) http://www.math.uiuc.edu/~jms/Papers/isama/color/
(23) http://arpam.free.fr/charbonneau.html
(24) http://arpam.free.fr/apery.htm
(25) http://publimath.irem.univ-mrs.fr/bibliocomp/IST99010.htm
(26) http://publimath.irem.univ-mrs.fr/bibliocomp/IST99003.htm
(27) http://www.math.uiuc.edu/~jms/Photos/MathArt/Maubeuge/
(28) http://new.math.uiuc.edu/five
(29) http://arpam.free.fr/jeener.html
(30) http://www.lactamme.polytechnique.fr
(31) http://www.apmep.asso.fr/
(32) http://www.xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.html
(33) http://arpam.free.fr/chavesforum.htm
(34) http://www.fc.up.pt/atractor
(35) http://weasel.cnrs.humboldt.edu/~spain/gran/other/image1.gif
(36) http://www.math.uiuc.edu/~jms/Photos/MathArt/Maubeuge/dickson-morin/
(37) http://perso.wanadoo.fr/jpq/
(38) http://www.vivagranada.com/images/alhambrabath1.jpg
(39) http://www.worldofescher.com/gallery/
(40) http://etab.ac-orleans-tours.fr/clg-mpagnol-vernouillet/Les%20pavages.htm
(41) http://arpam.free.fr/termes.html
(42) http://perso.wanadoo.fr/nvogel/index.html
(43) http://www.ac-noumea.nc/maths/amc/polyhedr/index.htm
(44) http://semsci.u-strasbg.fr/pavagede.htm
(45) http://serge.mehl.free.fr/anx/cristaux.html
(46) http://www.eduscol.education.fr/tpe/default.htm
(48) http://www.palais-decouverte.fr/
(49) http://irem.u-strasbg.fr/
(50) http://home.nordnet.fr/~eostenne/declic.htm